Standardform

Standardform er en måte å skrive veldig store eller veldig små tall på. Sjekk ut Standardform arbeidshefte

Reglene for standardform:

Tall skrives som et produkt av en desimal og en tierpotens: Et tall i standardform skrives som: a×10ⁿ hvor a er et tall mellom 1 og 10 (1 ≤ a < 10), og n er et heltall.
Positiv eksponent for store tall: Tallet 1000 kan skrives som 10³.
Negativ eksponent for små tall: I motsatt ende har vi svært små tall. Tallet 0.001 kan skrives som 10^-3. En annen skrivemåte er .

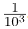For å skrive 314 på standardform, teller man hvor mange plasser komma skal flyttes. Det går i eksponenten.

Eks: 3,14 * 10².

For å forstå det lettere, kan det skrives på en annen måte: 3,14 * 100 = 314.

Det samme gjelder større tall. 1 240 000 = 1,24 * 1 000 000 = 1,24 * 10⁶.

For små tall flytter vi komma den andre veien. Da blir det et negativt tall i eksponenten. 0,000 004 560 = 4,56 * 10^-6.

På en annen måte kan det skrives:

Summering og divisjon av tall på standardform følger vanlige regler. Tall på standardform er fremdeles tall.

Når eksponentene er like, kan vi legge sammen og fremdeles bruke samme eksponent.

Eksempel: 1,2 * 10² + 2,5 * 10² = (1,2 + 2,5) * 10² = 3,7 * 10².

Når eksponentene er ulike, så må de gjøres like.

Eksempel: 2,5 * 10³ + 2,5 * 10² = 25 * 10² + 2,5 * 10² = (25 + 2,5) * 10² = 27,5 * 10².

De samme reglene gjelder ved subtraksjon.

Ved multiplikasjon og divisjon er det litt andre regler. Ved multiplikasjon multipliseres faktorene, og eksponentene legges sammen eller trekkes fra.

Eksempel: 4 * 10² * 3 * 10³ = 4 * 3 * 10² * 10³ = 4 * 3 * 10^{2 + 3} = 12 * 10⁵.

Ved divisjon trekkes tallet fra eksponenten.